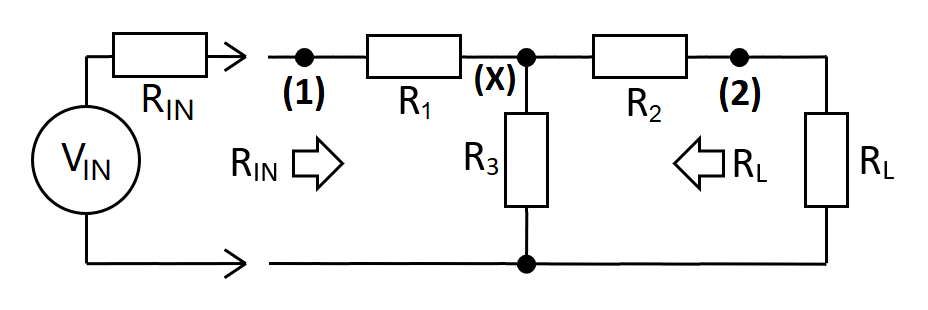
The taper-pad uses $R_1$, $R_2$ and $R_3$ to match $R_{IN}$ to $R_L$. Circuit gain ($A_{12}$) is from input (1) to output (2). For example, if $A_{12}$ is set to 0.25 then this is a 4:1 attenuation (-12.0412 dB).

$\hspace{9cm}$

Taper-pad attenuator Circuit

Relevant Formulas

_{$$A_{12(MAX)} = \frac{R_L}{R_{IN}}\left[1-\sqrt{1-\frac{R_{IN}}{R_L}}\text{ }\right]\hspace{0.5cm}R_L>R_{IN}$$} _{$$A_{12(MAX)} = 1-\sqrt{1-\frac{R_L}{R_{IN}}}\text{ }\hspace{2.0cm}R_{IN}>R_L$$}

_{$$R_1 = R_L\left[\dfrac{1 + \frac{R_{IN}}{R_L}A_{12}^2 - 2\cdot A_{12}}{\frac{R_L}{R_{IN}}- A_{12}^2}\right]$$

$$R_2 = R_L\left[\dfrac{\frac{R_L}{R_{IN}}+ A_{12}^2 - 2\cdot A_{12}}{\frac{R_L}{R_{IN}}- A_{12}^2}\right]$$

$$R_3 = R_L\left[\dfrac{2\cdot A_{12}}{\frac{R_L}{R_{IN}}- A_{12}^2}\right]$$}


_{$R_{IN}$}	_Ω	_{$\boxed{R_1=}$}	_Ω
_{$R_L$}	_Ω	_{$\boxed{R_2=}$}	_Ω
_{$A_{12}$}	_V/V	_{$\boxed{R_3=}$}	_Ω
_{$A_{12}\text{ (dB)}$}	_dB	_{$\boxed{A_{12(MAX)}=}$}	_V/V

_{Transfer values (applicable when analysing as two back-to-back L-Pads)}
_{_{$\hspace{1cm} R_X\hspace{1cm}=$}}	_{_Ω}	_{_{$\hspace{1cm} R_3\hspace{1cm}=$}}	_{_Ω}
_{_{$\hspace{1cm} R_{3A}\hspace{0.9cm}=$}}	_{_Ω}	_{_{$\hspace{1cm} R_{3B}\hspace{0.8cm}=$}}	_{_Ω}
_{_{$\hspace{1cm} A_{1X}\hspace{0.9cm}=$}}	_{_V/V}	_{_{$\hspace{1cm} A_{X2}\hspace{0.8cm}=$}}	_{_V/V}

Deriving the equations
To derive the above equations we need to look at the basic gain relationships. Then, we can move on to distill these equations by considering the transfer impedance of two back-to-back L-pads. Firstly we'll find equations for $R_1$, $R_2$ and $R_3$. These are indicated as (1), (2) and (3) directly below.

Basic gain equations

At point X, $R_3$ is in parallel with $R_2+R_L$ and forms a potential divider with $R_1$. Importantly, the sum of $R_1$ and $R_3||(R_2+R_L)$ equals $R_{IN}$ hence:

$$\hspace{3cm}A_{1X} = \dfrac{R_{IN}-R_1}{R_{IN}}\hspace{3cm}$$

The gain between X and the output is this:

$$A_{X2} = \dfrac{R_L}{R_L+R_2}$$

Therefore, the overall gain is: $A_{1X}\times A_{X2}$

$$A_{12}=\dfrac{R_L}{R_{IN}}\cdot\dfrac{R_{IN}-R_1}{R_L+R_2}\tag{0}$$

From (0) we can solve for $R_1$ and $R_2$:

$$R_1 = R_{IN}\cdot\left[1-\dfrac{R_L+R_2}{R_L}\cdot A_{12}\right]\tag{1}$$ $$R_2 = R_{L}\cdot\left[\dfrac{R_{IN}-R_1}{A_{12}\cdot R_{IN}}-1\right]\tag{2}$$

To find $R_3$: -

Solve $A_{1X}$ using $R_3$:

Noting that $R_{IN} = R_3||(R_2+R_L) + R_1$:

Multiply by $A_{X2} = \dfrac{R_L}{R_2+R_L}$ to obtain $A_{12}$:

Rearrange:

$$A_{1X}=\dfrac{R_3||(R_2+R_L)}{R_3||(R_2+R_L) + R_1}$$ $$A_{1X}=\dfrac{R_3||(R_2+R_L)}{R_{IN}}$$ $$A_{1X}=\dfrac{R_3\cdot(R_2+R_L)}{R_{IN}\cdot(R_2+R_3+R_L)}$$ $$A_{12}=\dfrac{R_L}{R_{IN}}\cdot\dfrac{R_3}{R_2+R_3+R_L}$$ $$$$ $$R_3=\dfrac{R_2+R_L}{\frac{R_L}{R_{IN}\cdot A_{12}}-1}\tag{3}$$

Transfer Impedance analysis

At this point, the formulas above are all interdependent so, as a means of distilling them, we formulate a second analysis. This means considering the transfer impedance ($R_X$): -

(1) Resistor $R_3$ is split into two parts (a and b)

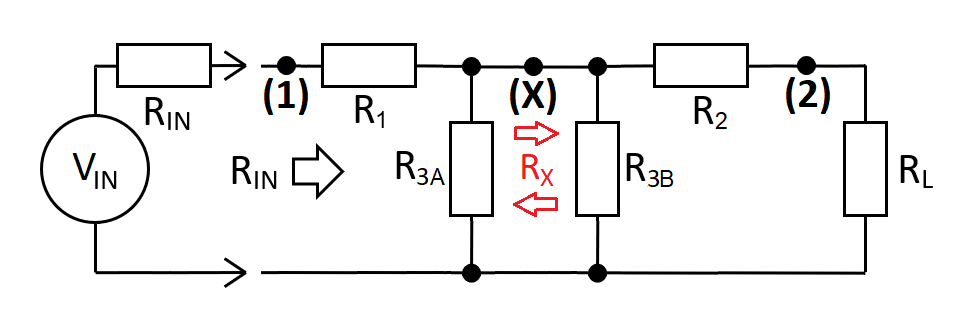
(2) Use formulas from the resistive matching L-pad

(3) Modify and apply to left and right sections.

For the left hand side
$$R_1=R_{IN}\sqrt{1-\dfrac{R_X}{R_{IN}}}\tag{4}$$ $$R_{3A} = \dfrac{R_{IN}\cdot R_X}{R_1}$$

For the right hand side
$$R_2=R_{L}\sqrt{1-\dfrac{R_X}{R_{L}}}\tag{5}$$ $$R_{3B} = \dfrac{R_{L}\cdot R_X}{R_2}$$

Using equation (4) $$R_X=\dfrac{R_{IN}^2-R_1^2}{R_{IN}}=\dfrac{(R_{IN} - R_1)(R_{IN} + R_1)}{R_{IN}}$$

Using equation (5) $$R_X=\dfrac{R_{L}^2-R_2^2}{R_{L}}=\dfrac{(R_{L} - R_2)(R_{L} + R_2)}{R_{L}}$$

Noting that $A_{1X} = \frac{R_{IN}-R_1}{R_{IN}}$,

$$R_X = A_{1X}\cdot (R_{IN} +R_1)$$

Noting that $A_{X2} = \frac{R_L}{R_L+R_2}$, $$R_X = \dfrac{R_L-R_2}{A_{X2}}$$

Equating the two above formulas together like this: -
$$A_{1X}\cdot (R_{IN} +R_1)= \dfrac{R_L-R_2}{A_{X2}}$$ $$A_{12}=\dfrac{R_L-R_2}{R_{IN}+R_1}\tag{6}$$ Then, we substitute in equation (6) for $R_2$ from equation (2): -
$$A_{12}=\dfrac{R_L-R_L\left[\dfrac{R_{IN}-R_1}{A_{12}\cdot R_{IN}}-1\right]}{R_{IN}+R_1}$$ $$A_{12}\cdot\dfrac{R_{IN}+R_1}{R_L} = 2 - \dfrac{R_{IN}-R_1}{A_{12}\cdot R_{IN}}$$ $$A_{12}^2\cdot\dfrac{R_{IN}}{R_L}\cdot (R_{IN}+R_1)=R_1+2\cdot A_{12}\cdot R_{IN}-R_{IN}$$ $$A_{12}^2\cdot\dfrac{R_{IN}^2}{R_L}=R_1\left[1-A_{12}^2\cdot\dfrac{R_{IN}}{R_L}\right]+R_{IN}\left[2\cdot A_{12}-1\right]$$ $$R_1 = \dfrac{A_{12}^2\cdot\frac{R_{IN}^2}{R_L}-R_{IN}\left[2\cdot A_{12}-1\right]}{1 - A_{12}^2\cdot\frac{R_{IN}}{R_L}} \hspace{1cm}=\hspace{1cm}R_L\left[\dfrac{1+A_{12}^2\cdot\frac{R_{IN}}{R_L}-2\cdot A_{12}}{\frac{R_L}{R_{IN}}-A_{12}^2}\right]\tag{7}$$

Micro-cap simulation analysis

The simulation below confirms the equations derived above. The scenario is for a 50 Ω input impedance and a 100 Ω output impedance having a gain ($A_{12}$) of 0.25: -

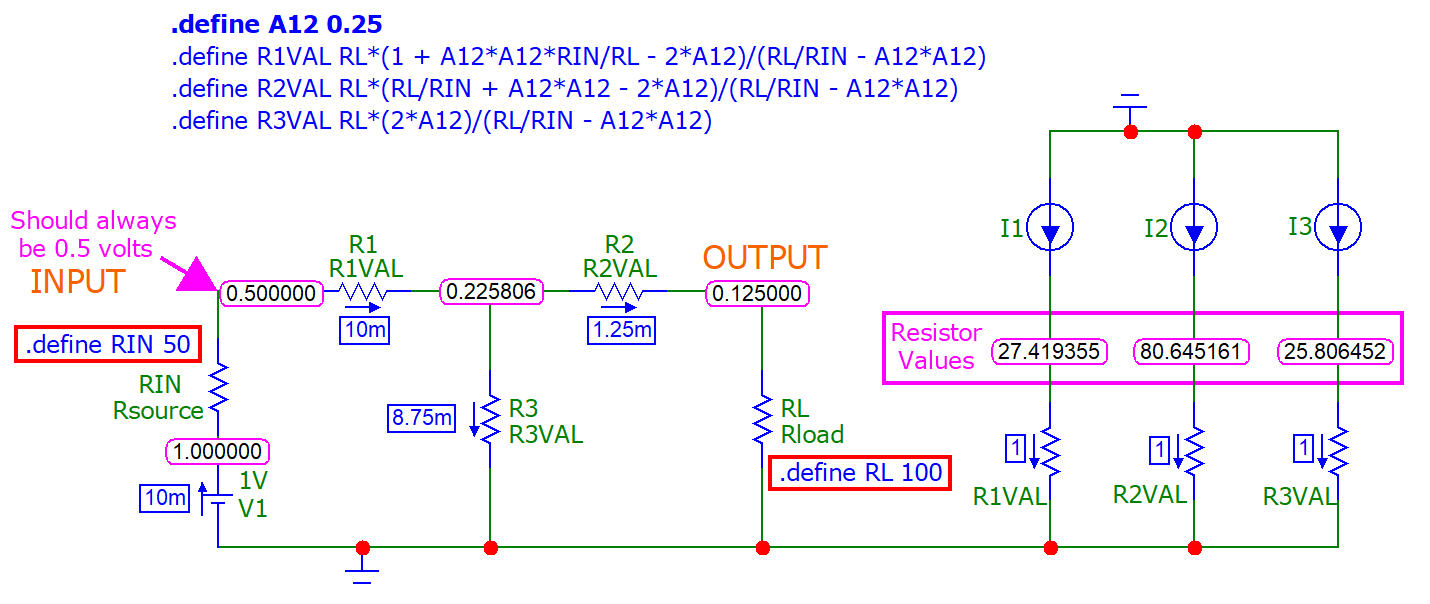
The source (V1) is reduced from 1 volt to 0.5 volts hence the input impedance is 50 Ω
The input is 0.5 volts and the output is 0.125 volts hence, $A_{12}$ = 0.25
1 amp current sources "test" the values of R1, R2 and R3 (to the right)
Those values match what the calculator produces at the top of this page