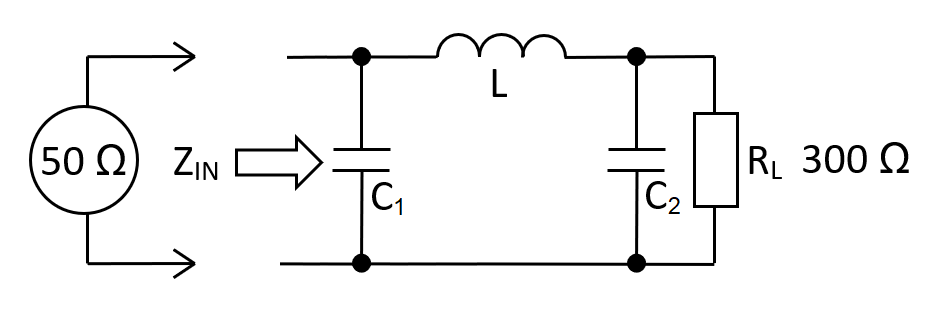
The low-pass \(\pi\) network is equivalent to a pair of back-to-back low-pass L-Pad networks: -
\(\hspace{18.9cm}\)
Low-pass \(\pi\) network
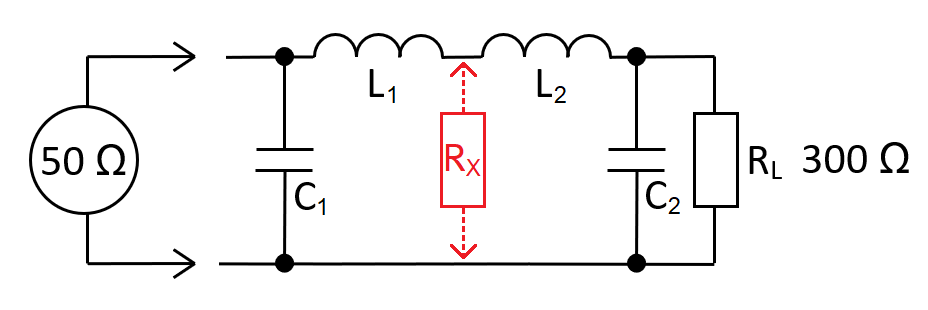
Equivalent circuit
\(C_1 = \dfrac{1}{\omega\cdot R_{IN}}\sqrt{\dfrac{R_{IN}}{\color{red}{R_X}}-1}\hspace{1cm} L_1 = C_1\cdot R_{IN}\cdot\color{red}{R_X} \)
\(C_2 = \dfrac{1}{\omega\cdot R_{L}}\sqrt{\dfrac{R_{L}}{\color{red}{R_X}}-1}\hspace{1.7cm} L_2 = C_2\cdot R_{L}\cdot\color{red}{R_X} \)
The equivalent circuit
RX represents \(R_L\) for the left-stage and \(R_{IN}\) for the right stage. You solve the left and right stages independently then combine L1 and L2 into inductor LT. RX is called the transfer impedance \(Z_T\).
The calculator below requires RX to be less than RIN. This makes L1 and C1 an impedance reducer with L2 and C2 as an impedance multiplier. With the \(\pi\) calculator's default values, 50 Ω is converted to a \(Z_T\) of 25 Ω and then \(Z_T\) is multiplied to 300 Ω.
| RIN: |
|
Ω |
| RX: |
|
Ω |
| RL: |
|
Ω |
| FIN: |
|
MHz |
| L1: | ÁH | |
| L2: | ÁH | |
| LT: | ÁH | |
| C1: | pF | |
| C2: | pF | |
|
AV at FIN:
Voltage gain from \(Z_{IN}\) to \(R_L\)
|
V/V |
The relevance of Q-factor
As previously proven for the basic L-Pad network, these relations are all true: - $$Q \hspace{0.5cm} = \hspace{0.5cm}A_V\hspace{0.5cm} = \hspace{0.5cm}\sqrt{\dfrac{R_L}{R_{IN}}}\hspace{0.5cm} = \hspace{0.5cm}R_L\sqrt{\dfrac{C}{L}}\hspace{0.5cm}=\hspace{0.5cm}\omega_n R_L C$$
This means that Q is not an input variable; it is wholly defined by \(R_{IN}\) and \(R_L\). However, because the \(\pi\) network has a transfer impedance, Q-factor has two identities. For this reason, Q is discarded as an input variable in favour of RX. \(A_V\) is still calculated based on a lossless power transfer: - $$A_V=\sqrt{\dfrac{R_L}{R_{IN}}}$$
Benefits of the \(\pi\) network
The 1st benefit is that you can manipulate the pass-bandwidth at the operating frequency. The image below shows the bode-plot response for several values of RX. The upper graph is gain and the lower graphs are \(\angle{Z_{IN}}\) and \(|Z_{IN}|\): -
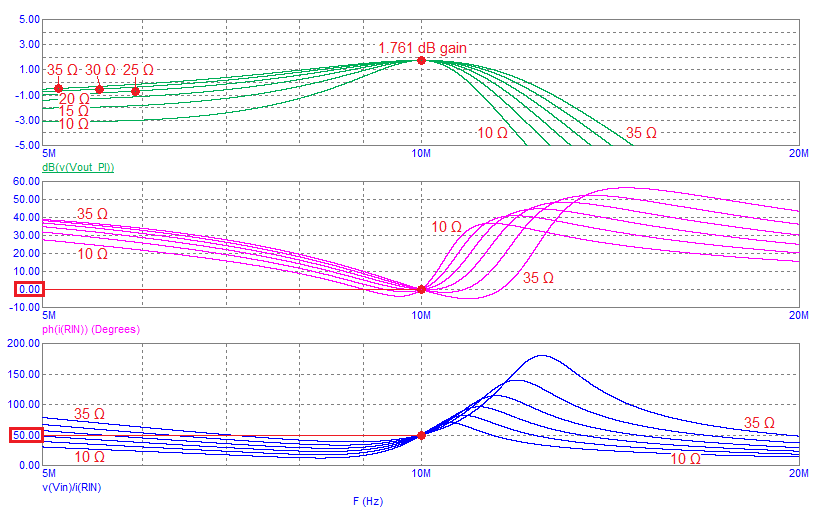
At 10 MHz, the gains converge at 1.761 dB. In real numbers that's 1.2247 and, when taking into account the 2:1 loss when connecting a 50 Ω source to a network with \(Z_{IN}\) = 50 Ω, the voltage magnification is the same as the low-pass L-Pad network (2.44949): -
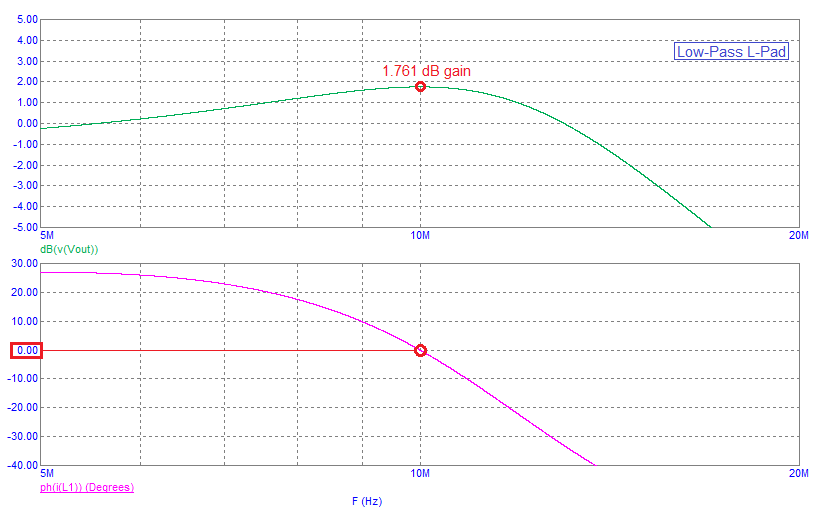
The 2nd benefit; The input impedance phase angle can be tailored to be more closely resistive than the L-Pad in the operating region around the centre frequency.
The 3rd benefit is that the input impedance and output impedance can be equal. This may not seem much of a benefit for an impedance transformer but, if you consider that several \(\pi\) networks can be cascaded to produce a significant filtering effect, you have a tool that is very useful.
The low-pass \(\pi\) network in cascade
Below is a 50 Ω to 50 Ω, 5-stage cascaded \(\pi\) network simulated in Micro-cap 12 (RX = 25 Ω): -
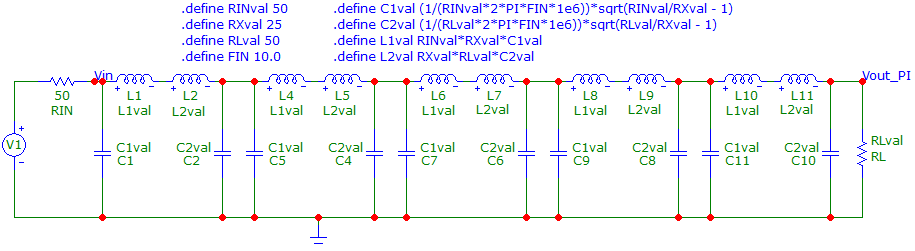
The frequency response, impedance phase angle and impedance magnitude is this: -
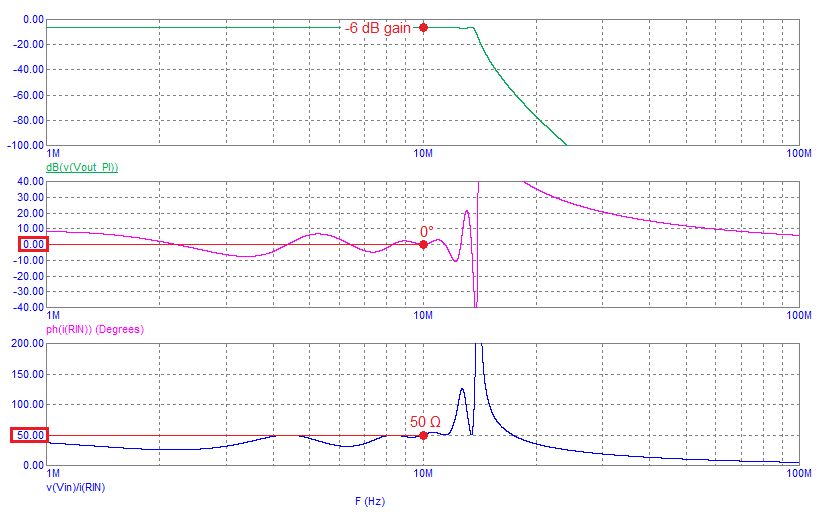
The main feature is the very sharp attenuation from about 13 MHz. The impedance is fairly flat from about 8 MHz to 11 MHz with the corresponding impedance phase angle remaining close to 0░.
When cascading \(\pi\) stages, the value calculations are repeated and trivial.