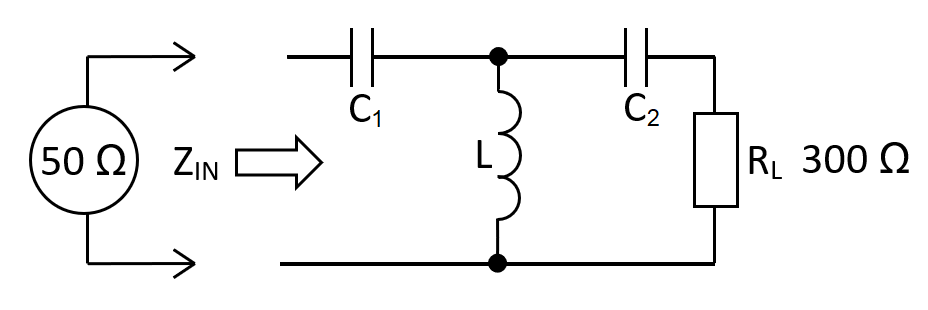
The high-pass T-network is equivalent to a pair of back-to-back high-pass L-Pad networks: -
\(\hspace{18.9cm}\)
High-pass T-network
Equivalent circuit
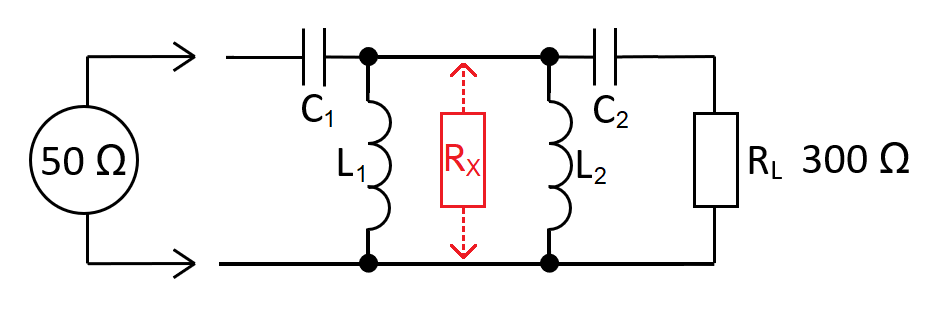
\(C_1 = \dfrac{1}{\omega\cdot R_{IN}}\sqrt{\dfrac{1}{\frac{\color{red}{R_X}}{R_{IN}}-1}}\hspace{1cm} L_1 = C_1\cdot R_{IN}\cdot \color{red}{R_X} \)
\(C_2 = \dfrac{1}{\omega\cdot R_{L}}\sqrt{\dfrac{1}{\frac{\color{red}{R_X}}{R_L}-1}}\hspace{1.7cm} L_2 = C_2\cdot R_{L}\cdot\color{red}{R_X} \)
The equivalent circuit
RX represents \(R_L\) for the left-stage and \(R_{IN}\) for the right stage. You solve the left and right stages independently then combine L1 and L2 into inductor LT. RX is called the transfer impedance \(Z_T\).
The calculator below requires RIN to be less than RX. This makes L1 and C1 an impedance multiplier with L2 and C2 as an impedance reducer. With the T calculator's default values, 50 Ω is converted to a \(Z_T\) of 1000 Ω and then \(Z_T\) is reduced to 300 Ω.
| RIN: |
|
Ω |
| RX: |
|
Ω |
| RL: |
|
Ω |
| FIN: |
|
MHz |
| L1: | ÁH | |
| L2: | ÁH | |
| LT: | ÁH | |
| C1: | pF | |
| C2: | pF | |
|
AV at FIN:
Voltage gain from \(Z_{IN}\) to \(R_L\)
|
V/V |
The relevance of Q-factor
As previously proven for the basic L-Pad network, these relations are all true: - $$Q \hspace{0.5cm} = \hspace{0.5cm}A_V\hspace{0.5cm} = \hspace{0.5cm}\sqrt{\dfrac{R_L}{R_{IN}}}\hspace{0.5cm} = \hspace{0.5cm}R_L\sqrt{\dfrac{C}{L}}\hspace{0.5cm}=\hspace{0.5cm}\omega_n R_L C$$
This means that Q is not an input variable; it is wholly defined by \(R_{IN}\) and \(R_L\). However, because the T-network has a transfer impedance, Q-factor has two identities. For this reason, Q is discarded as an input variable in favour of RX. \(A_V\) is still calculated based on a lossless power transfer: - $$A_V=\sqrt{\dfrac{R_L}{R_{IN}}}$$
Benefits of the T-network
The 1st benefit is that you can manipulate the pass-bandwidth at the operating frequency. The image below shows the bode-plot response for several values of RX. The upper graph is gain and the lower graphs are \(\angle{Z_{IN}}\) and \(|Z_{IN}|\): -
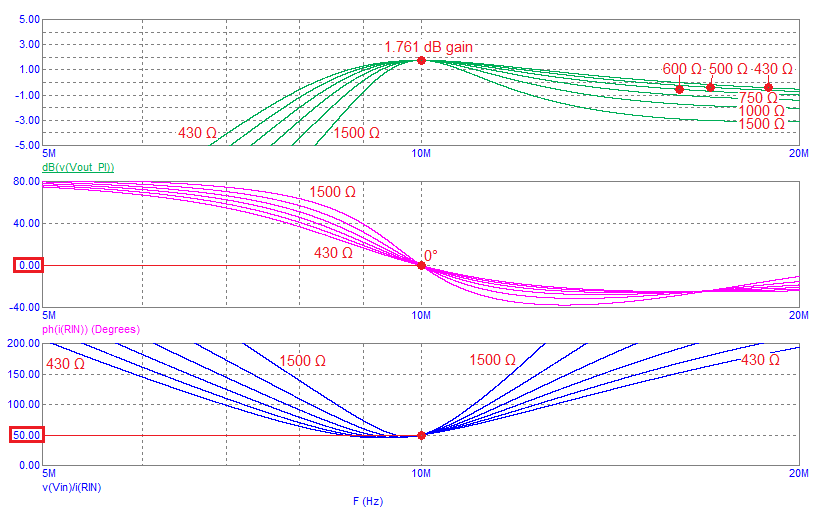
At 10 MHz, the gains converge at 1.761 dB. In real numbers that's 1.2247 and, when taking into account the 2:1 loss of connecting a 50 Ω source to a network with \(Z_{IN}\) = 50 Ω, the voltage magnification is the same as the high-pass L-Pad network (2.44949): -
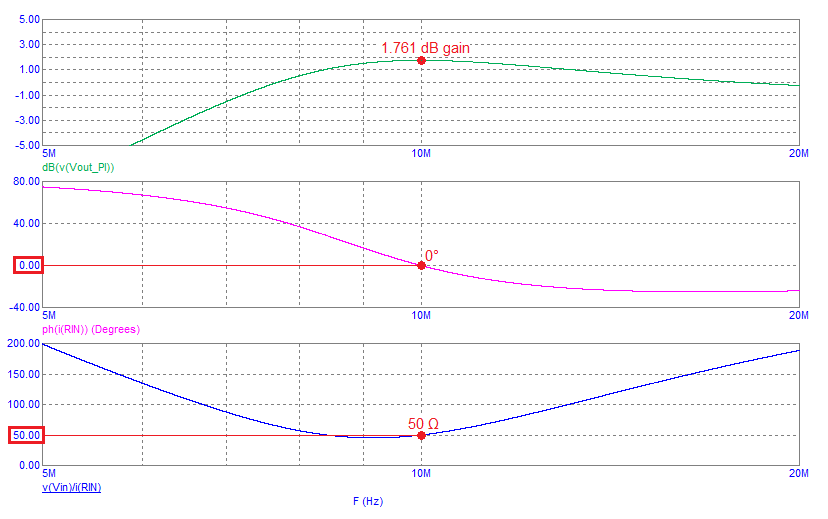
The 2nd benefit; The input impedance phase angle can be tailored to be more closely resistive than the L-Pad in the operating region around the centre frequency.
The 3rd benefit is that the input impedance and output impedance can be equal. This may not seem much of a benefit for an impedance transformer but, if you consider that several T-networks can be cascaded to produce a significant filtering effect, you have a tool that is very useful.
The high-pass T-network in cascade
Below is a 50 Ω to 50 Ω, 5-stage cascaded T-network simulated in Micro-cap 12 (RX = 100 Ω): -
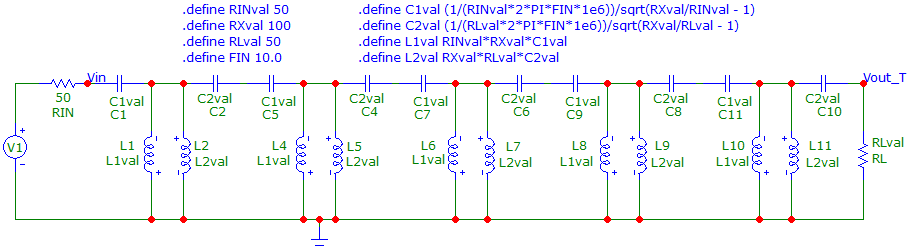
The frequency response, impedance phase angle and impedance magnitude are below: -
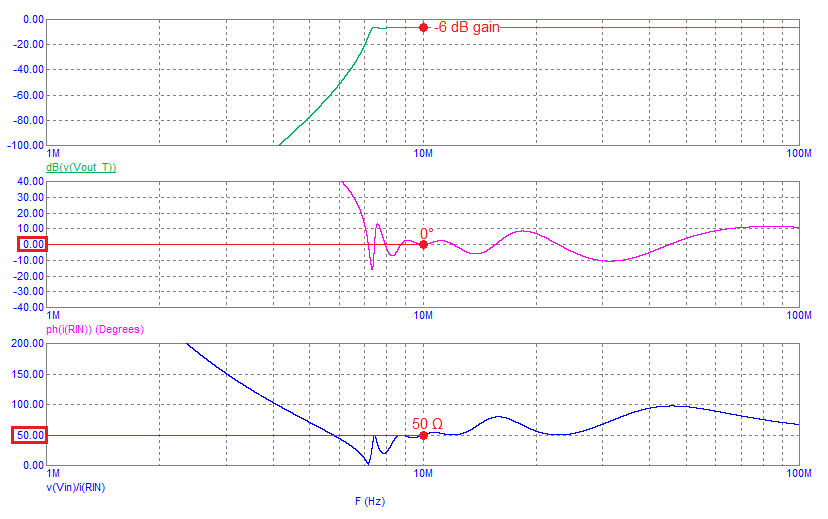
The main feature is the very sharp attenuation below about 7.5 MHz. \(Z_{IN}\) is fairly flat from about 8.5 MHz to 13 MHz with its corresponding phase angle remaining close to 0░ (resistive).
When cascading T stages, the value calculations are repeated and trivial.